Wiele osób powtarza pogląd, że „loterie są dla ludzi nierozumiejących praw statystyki”. Część na tym poprzestaje i nie gra. Część wypowiada te słowa, ale gra mimo to, mając nadzieję, że im się poszczęści. Jeśli chodzi o mnie, to ostatni raz „wysłałem totka” w 2011 roku na okoliczność rekordowej kumulacji, lecz przez te dziewięć lat co jakiś czas nawiedzały mnie myśli z „totkiem” (Lotto) związane. Przedstawiam część wniosków z moich dociekań.
Nie jestem matematykiem ani filozofem, a notka prezentuje tylko moje poglądy na omawiane tematy, które mogą ale nie muszą być prawdziwe. (Niestety większość jest.)
Zanim zaczniemy, artykuł do przeczytania: https://businessinsider.com.pl/firmy/totalizator-sportowy-pokazal-wyniki-sa-najlepsze-w-historii/b8w8w60
(W skrócie: Totalizator Sportowy w roku 2019 zarobił najwięcej pieniędzy w historii, ok. 11 mld zł.)
Spis treści
Co matematyka mówi na temat opłacalności?
Ruletka o czternastu milionach pól
Definicja opłacalności i systemu
Nadzieja matematyczna a opłacalność
Maksimum górnej granicy opłacalności
Postscriptum. Skomplikowane gwarancje
Przewidywanie wyniku gry
Zacznę od zagadnienia, które może wywołać uśmiech politowania. A jednak wielu graczy, powiedzmy, sceptycznych wobec nauki usiłuje przewidzieć, jakie kule zostaną wylosowane albo chociaż zawęzić zakres ich numerów — czyli z gry „wytypuj 6 z 49” zrobić grę „wytypuj 20 z 49”. Jak to uzasadniają?
Złudzenie kontroli
Wszystko to, co teraz opiszę, opiera się na złudzeniu, że jesteśmy w stanie kontrolować zjawiska leżące obiektywnie rzecz biorąc poza naszą kontrolą. Wyrazem tego złudzenia są często używane przez graczy stwierdzenia w rodzaju „Przewidzenie liczb jest trudne”, „Potrafię przewidzieć tyle a tyle liczb miesięcznie” itp.
Tymczasem punktem wyjścia każdych rozważań nie powinno być stwierdzenie, że dane zjawisko jest losowe i że wobec tego musi się ono zachowywać tak a tak. Stwierdzenie, że dane zjawisko jest losowe, jest konkluzją a nie aksjomatem. Jest konkluzją ogłaszaną w momencie, gdy widzimy, że nie umiemy przewidzieć przebiegu tego zjawiska. Mówiąc dobitnie: jeśli coś jest losowe, to znaczy to, że nie umiemy tego czegoś przewidzieć, a nie że na tej właśnie podstawie to coś przewidzimy, nawet z grubsza.
Oto pierwsze wyrazy ciągu liczb: 0, 5, 10, 15, 20. Czy jesteśmy w stanie przewidzieć następne? Nie.
To, jakie równanie kryje się za owymi liczbami — i czy w ogóle jakieś się kryje — zależy od tego, w wyniku jakiego zjawiska fizycznego czy innego powstał ów ciąg. Jeśli tego nie wiemy, to nie mamy możliwości niczego przewidzieć. Można co najwyżej się założyć — i trafić albo spudłować. (Nawet jeśli się trafi, nie znaczy to, że cokolwiek się przewidziało, żeby bowiem móc nazwać coś przewidywaniem, to coś musi się opierać na wiedzy a nie na zgadywaniu.)
Następnym wyrazem może oczywiście być 25, ale może nim być i 21. Dwadzieścia jeden? Ano tak. Specjalnie pogrzebałem w encyklopedii ciągów OEIS, aby znaleźć taki nieoczywisty przykład. Ciąg, o którym mowa, powstaje z zamiany danej liczby n oraz jej czterokrotności 4n na system dwójkowy i wzięcia sumy bitowej tych dwóch liczb. Np. dla n=4 mamy:
(n) OR (4n) = 4 OR 16 = (100)2 OR (10000)2 = (10100)2 = 20
Dla n=5 mamy:
(n) OR (4n) = 5 OR 20 = (101)2 OR (10100)2 = (10101)2 = 21
Kilka następnych wyrazów to: 30, 31, 40, 45, 42, 47. Wspaniała regularność się zaburza, prawda?
Wracając do loterii: nawet gdyby kolejne wyniki losowania były ze sobą powiązane (a nie są), i nawet gdyby na pozór pasowały do jakiegoś prostego wzoru, np. {1, 3, 5, 7, 9, 11}, {13, 15, 17, 19, 21, 23}, to i tak nie mielibyśmy pewności, że następne wyniki dalej będą do tego wzoru pasować. To tyle jeśli chodzi o matematyczne wróżenie z fusów.
Koncepcja mechanicystyczna
Skoro maszyna losująca jest obiektem fizycznym, to musi podlegać prawom mechaniki, z których da się wywieść ruchy wszystkich jej elementów, więc także i trajektorie kul.
Choć w teorii słuszny, w praktyce ów pogląd nie ma większego znaczenia, bowiem już zderzenie trzech dysków (nawet nie kul) na płaszczyźnie jest nietrywialnym, do dziś analizowanym problemem. Krótko mówiąc, gdybyśmy mieli wystarczającą liczbę czujników ruchu, nacisku i podobnego sprzętu, moglibyśmy przewidzieć efekt zderzenia trzech dysków albo kul na stole bilardowym tylko w przybliżeniu. Tutaj mamy zaś 49 kul w przestrzeni (nie na płaszczyźnie) i zupełny brak informacji z jakichkolwiek czujników. Zresztą na niewiele by się te informacje zdały, skoro zakłady zawieramy przed losowaniem a nie w trakcie losowania.
Koncepcja irracjonalistyczna
Są tacy, którzy wierzą w „sprawiedliwość” Losu. Zgodnie z wykładnią tej wiary, Los powinien czuwać nad tym, żeby kule wypadały mniej więcej równą liczbę razy.
I czuwa. Im dłużej będziemy losować, tym procentowe liczby wystąpień wszystkich kul będą bliższe 1/49*100%. Ale nie ma możliwości wywiedzenia z tego informacji, kiedy poszczególne kule będą wypadać. Gdyby Pan Los był tak „sprawiedliwy”, że w pierwszej kolejności likwidowałby różnice między liczbami wystąpień kul, to trudno zrozumieć, czemu w ogóle miałby dopuścić do powstania tych różnic.
A zatem: choć nie da się obalić wiary w „sprawiedliwość” Losu, można wykazać, że albo jest ona niespójna sama ze sobą („dzisiaj Pan Los wyrównuje krzywdy, jakie wyrządził kulom wybierając jedne częściej a inne rzadziej, ale wcześniej sam te krzywdy wyrządzał”) albo też nic z niej nie wynika („jeśli Pan Los raz jest sprawiedliwy a raz nie, to problemem staje się przewidzenie, którego dnia jaki będzie miał humor”).
Koncepcja spiskowa
Mamy oczywiście wśród graczy amatorów teorii spiskowych, których to teorii z oszczędności miejsca nie będę przytaczał. Można na własną rękę sprawdzić, jakie firmy dostarczają Totalizatorowi oraz jego odpowiednikom w innych krajach maszyn do losowania. Firmy te działają od wielu lat, więc wszelkie oszustwa przy budowie maszyn prędzej czy później ujrzałyby światło dzienne (z powodu rotacji pracowników, lukratywności ujawniania tego typu informacji tabloidom itp.). Kiedyś próbowałem dowiedzieć się więcej o jednej z takich firm, działającej w jakimś brytyjskim miasteczku, lecz to bezsens. Jak się za chwilę okaże, Totalizator naprawdę nie musi oszukiwać przy loterii, bo jej zasady są tak skonstruowane, że przy ich przestrzeganiu zapewnia ona w miarę stały strumień dochodów.
Brak koncepcji
Co do wróżenia numerów kul ze snów i podobnych praktyk, cóż… Zauważę tylko, że wiele osób ma wiele snów. Nie sądzę żeby wszyscy śnili o tym samym, zatem wyśnione liczby będą z pewnością dla każdego inne. Skąd wiesz, czyj sen będzie rekonstruował dziś Pan Los?
Oswajanie prawdopodobieństwa
Dawno temu przeczytałem w mądrej książce, że statystyka wcale nie miała łatwo w początkowych latach swego istnienia. Pojęcie prawdopodobieństwa, podobnie jak na przykład pojęcie prędkości w mechanice, napotykało niezrozumienie i opór, stąd też rozsądnie będzie parę zdań o nim powiedzieć.
Mówimy o prawdopodobieństwie w rozumieniu klasycznym, takim, jakiego uczymy się w liceum i jakie będzie nam potrzebne do analizy gier liczbowych. Otóż jeśli jakieś zdarzenie w dłuższym przeciągu czasu wydarza się z pewną regularnością, możemy podzielić liczbę wystąpień tego wydarzenia przez liczbę sytuacji, gdy to wydarzenie miało możliwość wystąpić. Jeśli na przykład wiemy ze statystyk, że średnio jeden na sto rowerów pada łupem złodziei, to prawdopodobieństwo, że ktoś ukradnie mi rower, wynosi 1%. Wiedza ta pozwala działać towarzystwom ubezpieczeniowym.
A więc jeśli trudno nam operować na procentach prawdopodobieństwa, pomyślmy o nich jako o liczbie rzeczywiście istniejących obiektów lub zdarzeń spełniających jakieś kryteria — w stosunku do wszystkich obiektów bądź zdarzeń.
Drugim zagadnieniem jest równoprawdopodobieństwo. Usłyszałem kiedyś w „Rozmowach w toku”, że trzeba do ludzi zagadywać, bo jeśli nie zagadasz — masz zero procent szans na zakolegowanie się, a jeśli zagadasz — masz 50% szans. „Czemu 50%? — pyta uczestnik programu. — No bo albo cię polubi albo nie polubi”. To nieporozumienie.
Jeśli wylecę z okna na pierwszym piętrze, to nie mam tylko 50% szans na przeżycie. Tak samo jeśli wylecę z piętra dziesiątego — na pewno moje szanse nie są na poziomie 50%. Liczby, których stosunek wchodzi tu w grę, to liczba osób które przeżyły upadek z pierwszego i dziesiątego piętra oraz liczba osób, które w ogóle wypadły z okna na tych piętrach. Nigdy nie możemy zakładać, że pewne zdarzenia są równoprawdopodobne.
W grach liczbowych jest inaczej. Maszyny losujące są kalibrowane tak, by wyniki losowań rzeczywiście były równoprawdopodobne i tego założenia będziemy się trzymać. Wynika z niego w szczególności, że wypadnięcie każdej liczby jest tak samo prawdopodobne.
Co matematyka mówi na temat opłacalności?
A teraz najciekawsza część notki. Czy gra na loterii może być opłacalna? Nie. No dobrze, to było do przewidzenia, bo jak wiemy jedynym graczem, który na niej zarabia, jest jej organizator. Ale właściwie dlaczego?
Ruletka o czternastu milionach pól
Wyobraźmy sobie ruletkę o czternastu milionach pól. Na każdym polu wypisana jest inna kombinacja 6 z 49 liczb. W tej ruletce jest tylko jedna kulka, ale gra jest funkcjonalnym odpowiednikiem Lotto — każdy jej wynik odpowiada innemu i tylko jednemu wynikowi Lotto, a przebieg gry jest równie nieprzewidywalny. Już w tym miejscu część graczy zaprotestuje, więc proszę o chwilę zastanowienia i przetrawienie tego faktu we własnym zakresie.
Teraz następny element puzzli. Płacimy krupierowi 3 złote a on kładzie na odpowiednim polu na stole do gry żeton. Ale nie tylko ten jeden żeton! Żetony są różne: szóstkowe, piątkowe, czwórkowe, trójkowe. Krupier na wskazanym przez nas polu kładzie jeden żeton szóstkowy, zaś na innych polach — po jednym na pole — kładzie łącznie 258 żetonów piątkowych, paręnaście tysięcy żetonów czwórkowych i ćwierć miliona żetonów trójkowych. Skąd się te liczby biorą? Obliczamy, na ilu polach ruletki wydrukowane są kombinacje mające wspólne wszystkie sześć liczb z naszą kombinacją (za którą zapłaciliśmy krupierowi). Cóż, na jednym. A co z kombinacjami mającymi pięć wspólnych liczb? Żeby stworzyć kombinację mającą pięć wspólnych liczb z naszą, musimy najpierw wybrać, które pięć liczb z naszego zakładu będzie wspólnych (wybieramy 5 z 6 liczb, →współczynnik dwumianowy) — a następnie dobrać jedną liczbę z pozostałych w puli (wybieramy 1 z 43 liczb). Analogicznie dla czwórek i trójek.
Wszystko to jest warte paręnaście milionów złotych, ale niech nas ta liczba nie zmyli, gdyż nie możemy wygrać wszystkiego na raz, a gdybyśmy nawet chcieli zagwarantować wygranie wszystkiego na raz, musielibyśmy wyłożyć parę razy więcej. Ile dokładnie? Wbrew pozorom, odpowiedź na to pytanie ma znaczenie, przyjrzyjmy się więc problemowi bliżej.
Definicja opłacalności i systemu
Zaproponuję teraz następującą definicję opłacalności gry. A zatem: powiedzieć, że coś „się opłaca” to powiedzieć tyle, że coś „płaci samo za siebie”, czyli że na danym przedsięwzięciu nie tracimy.
Opłacalność gry to prawdopodobieństwo niestracenia pieniędzy na grze danym systemem. System to zbiór zakładów zawartych na to samo losowanie przez tego samego gracza.
Zgodnie z definicją, opłacalność jest to stosunek liczby wyników gry (pól ruletki), przy których wygramy co najmniej tyle, ile zainwestowaliśmy, do liczby wszystkich wyników gry. Przyznaję, że dla systemów wielozakładowych ręcznie jest z tym za dużo liczenia. Napisałem prosty program, który w kilkanaście sekund tworzy tabelkę wszystkich możliwych kombinacji wygranych (np.: trzy trójki, dwie czwórki, zero piątek i jedna szóstka) oraz zlicza, ile wyników losowania im sprzyja. Wyniki jego analiz znajdą się przy końcu notki.
Nadzieja matematyczna
Teraz przeczytajcie artykuł matematyka, Bartosza Żółtaka: http://www.permutu.pl/blog/lotto/ Oblicza on tzw. wartość oczekiwaną (zwaną też nadzieją matematyczną) dla Lotto.
W skrócie: jeśli przemnożymy każdą możliwą wypłatę (wartość żetonów na danym polu) przez prawdopodobieństwo jej uzyskania i zsumujemy otrzymane w ten sposób liczby, otrzymamy wynik znacząco mniejszy od kosztu zawarcia zakładu, który daje nam prawo udziału w loterii. Znaczy to, że Totalizator więcej pieniędzy zatrzymuje niż wypłaca graczom. Innymi słowy, w perspektywie lat, procent zwrotu z naszej totolotkowej „inwestycji” będzie taki sam, obojętnie czy gramy jednym zakładem czy milionem zakładów i będzie wynosił 25–35% w zależności od kwot płaconych za szóstkę, piątkę i czwórkę — krótko mówiąc, znaczną część pieniędzy stracimy. Alternatywnie można powiedzieć, że jeśli obstawilibyśmy wszystkie możliwe zakłady, to wartość wygranych stanowiłaby taki właśnie procent poniesionych kosztów.
Nadzieja matematyczna a opłacalność
Przyznaję, że z początku uważałem nadzieję matematyczną za mało przydatny z punktu widzenia gracza wskaźnik. Jej wartość zależy bowiem od wartości szóstki, a ta nie ma większego znaczenia dla przeciętnego gracza. (Ważne, żeby tę szóstkę wygrać.)
A jednak, owa wartość jest bardzo zgrubnym przybliżeniem maksymalnej możliwej do osiągnięcia opłacalności gry. Zauważmy, że gdyby dało się dzielić żetony na mniejsze cząstki albo też gdybyśmy dysponowali tylko żetonami o wartości równej kosztowi zakładu — to jest pierwsze założenie — oraz że gdybyśmy mogli te żetony układać zupełnie dowolnie na polach — to jest drugie założenie — to wtedy moglibyśmy rozłożyć żetony tak, aby suma ich wartości na każdym polu była dokładnie równa kosztowi gry. Wtedy właśnie tylko owe 25–35% pól byłoby zajętych.
Oznacza to, że gra byłaby — z punktu widzenia nadziei matematycznej — równoważna następującej: wpłacasz dowolną sumę pieniędzy, następnie rzucasz dwa razy monetą; jeśli dostaniesz dwa orły, odbierasz swoje pieniądze, jeśli nie — tracisz wszystko. Kiepski interes, nieprawdaż?
Drugi wniosek jest taki, że nawet najlepszy system nigdy nie osiągnie 25–35% opłacalności.
Systemy, systemiki…
Kiedy tylko poczujemy zapach pieniędzy, kupujemy u krupiera następny zakład. O ile w przypadku jednego zakładu było kompletnie obojętne, którą kombinację wybierzemy, o tyle na etapie drugiego zakładu mamy już pewien wpływ na rozkład naszych wygranych.
Po pierwsze zauważmy, że nadzieja matematyczna zwana też wartością oczekiwaną, obliczona przez p. Żółtaka, nie zmienia się. Jest to oczywiste, kiedy uświadomimy sobie, że zawarcie każdego nowego zakładu powoduje dołożenie tej samej liczby żetonów na pola naszej wyobrażonej ruletki. Zatem zwiększenie stawki (kupienie nowego zakładu) powoduje proporcjonalne zwiększenie pieniędzy do wygrania leżących na stole do gry. Szału nie ma.
Ale zauważmy też, że kiedy zawieramy drugi zakład, to mamy wpływ na to, gdzie dokładnie znajdzie się ćwierć miliona nowych żetonów. Pozycje tych żetonów są oczywiście ściśle związane z pozycją kombinacji, o wypadnięcie której się zakładamy (z pozycją żetonu szóstkowego). Możemy sobie wyobrazić to powiązanie w formie różnych kształtów, na przykład gwiazdy, czyli szeregu pól odchodzących w różnych kierunkach od jakiegoś centralnego pola. Jest to oczywiście uproszczenie, bo aby móc w ogóle mówić o tego typu wizualizacjach, musielibyśmy się poruszać zapewne w przestrzeni sześciowymiarowej — niemniej ma ono do odegrania ważną rolę.
Wyobraźmy sobie więc, że obstawione pola na ruletce układają się w gwiazdę. Zawierając drugi zakład, kładziemy na ruletkę drugą gwiazdę. Gwiazda ma to do siebie, że między jej wierzchołkami są przerwy — puste pola ruletki. To od nas zależy, o jaki kąt względem pierwszej „obrócona” będzie nasza druga gwiazda oraz ile z jej wierzchołków (w których są żetony) nałoży się na wierzchołki pierwszej gwiazdy.
Mamy zatem możliwość obrócić drugą gwiazdę tak, by liczba pustych pól ruletki była większa lub mniejsza. Jeśli jest większa, to większe jest prawdopodobieństwo, że niczego nie wygramy, ale za to jeśli już coś wygramy, to wygrana będzie większa. Jeśli pustych pól jest mniej, to mamy większe szanse na wygranie mniejszej sumy. Manipulujemy tzw. odchyleniem standardowym naszego rozkładu.
Żeby zmaksymalizować opłacalność systemu, musimy jak najrównomierniej rozłożyć żetony na polach ruletki, pamiętając o tym, by wartość żetonów na każdym polu nie była niższa od kosztu gry. Jak to zrobić, jest pytaniem otwartym.
Górna granica opłacalności
Określmy maksymalną opłacalność systemu w zależności od liczby jego zakładów, przy założeniu, że gramy systemem optymalnym. Co to znaczy? Nie znaczy to, że jego opłacalność wynosi 100%. Znaczy to, że nie ma w nim żetonów „zmarnowanych”, czyli takich, które leżą gdzieś na kupie i nie przyczyniają się do wzrostu opłacalności. Żeton jest zmarnowany, gdy można go przemieścić na inne pole nie zmniejszając wygranej na pierwotnym polu do wartości nieopłacalnej (mniejszej od kosztu systemu).
Na rysunku żetony zmarnowane to te leżące powyżej linii przerywanej. Rysunek przedstawia fragmenty dwóch systemów: po lewej stronie system nieoptymalny pod względem maksymalizacji opłacalności, po prawej — zoptymalizowany.
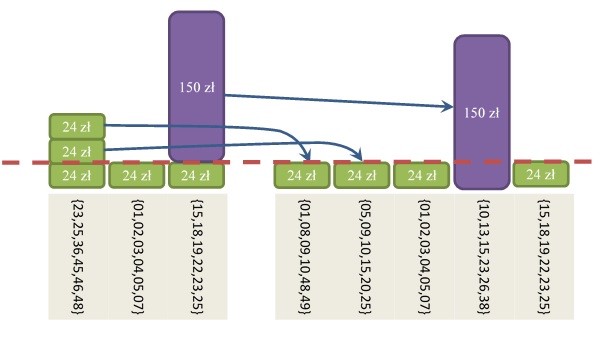
Rysunek 1.
Od razu zaznaczam, że systemy tak dobrze zoptymalizowane nie istnieją. Poniższe obliczenia są więc tylko przybliżeniem.
Gdyby można było pomnażać zawarte zakłady, nie zwiększając przy tym kosztu systemu, to liczba pól z żetonami stopnia n-tego (np. dla trójkowych n=3) wynosiłaby
(z oznacza liczbę zakładów). Niestety, trzeba się liczyć z tym, że większa liczba zakładów kosztuje więcej, czyli — co ważne z naszego punktu widzenia — większa liczba zakładów wymaga, by żetony były nałożone jeden na drugi. Nadal nie chcemy nakładać żetonów niepotrzebnie, więc to, co powiedzieliśmy wcześniej pozostaje w mocy. Po prostu przerywana linia z rysunku jest teraz odpowiednio wyżej, tak że mieszczą się pod nią np. dwa żetony. Nadal nie chcemy przechowywać żetonów powyżej tej linii.
Dlatego też powyższą liczbę musimy podzielić na tyle, ile żetonów danego rodzaju rekompensuje koszt systemu. Nie obejdzie się bez funkcji zaokrąglania z nadmiarem (tzw. sufit):
Symbolem xn oznaczyłem stosunek wartości żetonu do wartości jednego zakładu, np. dla żetonu trójkowego wynosi on 24 zł / 3 zł = 8.
Ostatecznie górna granica opłacalności (GGO) będzie sumą takich ilorazów dla piątek, czwórek i trójek. Z szóstkami sprawa wygląda inaczej, bo szóstki nie mogą się nałożyć na to samo pole i dać większej kwoty wygranej. Szóstki zatem muszą stać samotnie na swoich polach. W momencie, gdy koszt systemu przekracza wartość pieniężną szóstki, wszystkie nasze żetony szóstkowe muszą otrzymać inne żetony do towarzystwa lub zniknąć, niejako „utonąć” pod przerywaną linią — sprawa robi się nietrywialna, dlatego umówimy się, że będziemy eksplorować problem opłacalności tylko w zakresie systemów tańszych niż 2 mln zł, co jest chyba rozsądną umową.
Zachęcam Czytelnika do niezależnego sprawdzenia poprawności moich obliczeń:
Równanie 1.
Oto wykres maksymalnej opłacalności w funkcji kosztu systemu (przy założeniu 280 zł za czwórkę):

Rysunek 2.
Skąd te schody? Z funkcji zaokrąglania. Zgodnie z przewidywaniami, opłacalność rośnie wraz ze wzrostem liczby zakładów aż do pierwszego schodka, który następuje przy 9-zakładowym systemie. Ośmiozakładowy system może bowiem być zrekompensowany jedną trójką, dziewięciozakładowy — już nie. Stąd żetony trójkowe w systemie dziewięciozakładowym muszą być ułożone jeden na drugim. Spada liczba obstawionych żetonami trójkowymi pól „ruletki” i wraz z nią — prawdopodobieństwo pokrycia kosztów gry.
Większe schody pochodzą od nagród wyższych stopni (na wykresie powyżej widać tylko czwórki). Im większa kwota za wygraną wyższego stopnia, tym dłuższe (nie wyższe) stopnie tych schodów.
Maksimum górnej granicy opłacalności
Pytanie: wydaje się, że schodki zbiegają do jakiejś wartości leżącej w okolicach 20–25%, ale czy tak jest naprawdę? Ile wynosi największa z maksymalnych opłacalności? (To pytanie brzmi trochę dziwnie, ale przypominam, że wykres pokazuje teoretyczną maksymalną opłacalność dla danej liczby zakładów, co oznacza dla przykładu że jakichkolwiek ośmiu zakładów byśmy nie zawarli, nigdy nie otrzymamy systemu, który daje prawdopodobieństwo niestracenia pieniędzy większe od 14,91%. Teraz szukamy liczby zakładów, dla której te procenty są największe.)
Jeśli we wzorze powyżej (Równanie 1) opuścimy funkcję sufit, to będzie można wyeliminować liczbę zakładów w trzech największych składnikach sumy (pochodzących od trójek, czwórek i piątek). Zatem opłacalność będzie wtedy praktycznie stała dla każdego systemu! Jak bardzo taka operacja zafałszowuje wynik? Cóż, jeśli liczba zakładów będzie wielokrotnością wszystkich współczynników xn, to o zaokrąglaniu nie ma mowy, więc funkcję sufit można spokojnie opuścić i żadnego zafałszowania nie ma. Dla pozostałych przypadków funkcja zawyża wartość opłacalności, co nie powinno nam przeszkadzać, bo i tak szukamy górnego ograniczenia. Otrzymujemy:
Dla czwórki wartej 240 zł i piątki wartej 4800 zł daje nam to: 24,82% + z/13983816∙100%. Ostatni człon można właściwie pominąć, bo daje bardzo mały wkład w wynik (np. wartość jednego punktu procentowego osiągnie on przy 140 tys. zakładów). Zatem ~25% to rzeczywiście górna granica teoretycznej opłacalności przy podanych wartościach piątki i czwórki.
Oczywiście jeśli będziemy rozważać jakieś nieskończone kumulacje i inne teoretyczne twory, to żetony szóstkowe w końcu zapełnią wszystkie puste pola ruletki i opłacalność osiągnie 100%. Swoją drogą, ciekawe, ile musiałaby wynosić kumulacja, by to wszystko spłacić? Musielibyśmy położyć na stole (1 – 0,2482) ∙ 13983816 żetonów szóstkowych, czyli koszt takiego systemu wyniósłby ok. 32 miliony złotych i taka musiałaby być wartość szóstki. Zaznaczam, że to nie są obliczenia dotyczące wykupywania wszystkich zakładów (w takim bowiem przypadku musielibyśmy mieć kumulację 42 mln i pewność, że nikt inny szóstki nie trafi).
Wnioski i przykłady systemów
Wniosek jest oczywisty: grając nawet prawie idealnym i zapewne drogim systemem, mamy trzykrotnie większą szansę na stratę pieniędzy niż na osiągnięcie zysku lub wyjście na zero. To wyliczenie tyczy się każdej ilości losowań: jednego, dwóch, …miliona. Nie jest to zbyt optymistyczna prognoza. Ponadto, szansa, że w ciągu losowań nie stracimy ani złotówki bardzo szybko (wykładniczo) maleje do zera. Jeśli dla jednego losowania wynosi 25%, to dla dwóch jest to już 6%, dla trzech 2%, dla czterech — pół procenta. Naturalnie, otwarte pozostaje pytanie o saldo po kilku grach. Dla każdego systemu możliwe salda i ich prawdopodobieństwa będą inne. Do ich obliczenia trzeba najpierw sporządzić tabelę wygranych, o której wspomniałem już przy okazji definicji opłacalności a która pojawi się nieco dalej w notce.
Czas na parę realnych a nie teoretycznych danych. Poniżej zestawienie z kilkoma systemami oraz ich opłacalnością. Liczę na domyślność Czytelnika w kwestii znaczenia 49 kolumn i 6 krzyżyków w każdym wierszu.
Rozpoczniemy od systemu o największej opłacalności.
Koszt 0 zł, opłacalność: 100%
☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
System pusty na zero skreśleń. To — myślę — bardzo pouczający żart. Parafrazując slogan Totalizatora: „By nie przegrać, trzeba nie grać”.
Następny wynik właściwie już obliczyliśmy wcześniej (ćwierć miliona podzielić przez 14 milionów), ale zweryfikujmy jego poprawność moim programem.
Koszt 3 zł, opłacalność: 1,86%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
Zgadza się. Teraz wszystkie możliwe systemy dwuzakładowe:
Koszt 6 zł, opłacalność: 2,68%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☒☒☒☒☒☐☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
Koszt 6 zł, opłacalność: 3,17%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☒☒☒☒☐☐☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
Koszt 6 zł, opłacalność: 3,44%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☒☒☒☐☐☐☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
Koszt 6 zł, opłacalność: 3,61%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☒☒☐☐☐☐☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
Koszt 6 zł, opłacalność: 3,70%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☒☐☐☐☐☐☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
Koszt 6 zł, opłacalność: 3,72%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☐☐☐☐☐☐☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
Jak widać, im więcej liczb występuje w systemie, tym więcej pól naszej wirtualnej ruletki pokrywamy — nic nowego, czego byśmy nie wiedzieli. Dysponując tą wiedzą, przeanalizujemy tylko jeden, najbardziej opłacalny system ośmiozakładowy:
Koszt 24 zł, opłacalność: 14,83%
☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☐☐☐☐☐☐☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☐☐☐☐☐☐☐☐☐☐☐☐☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐
☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☒☒☒☒☒☒☐☐☐☐☐☐☐☐☐☐☐☐☐
☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☒☒☒☒☒☒☐☐☐☐☐☐☐
☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☐☒☒☒☒☒☒☐
Maksymalna opłacalność w teorii wyszła równa 14,91%. Jak widać, jest ona nieosiągalna. Czemu? Niestety, w powyższym systemie 11200 pól ruletki obłożonych jest dwoma żetonami trójkowymi. Dla przykładu, wypadnięcie kombinacji {1,2,3,7,8,9} spowoduje wygranie trójki w pierwszym i w drugim zakładzie. Skąd 11200? Wybieramy 2 zakłady z 8, następnie dwukrotnie po 3 liczby z 6 i otrzymujemy 11200 kombinacji. Proste i nieuniknione. Takie to mamy rozbieżności między teorią a praktyką.
Mamy osiem zakładów, potem mamy dziewięć zakładów. Tu następuje schodek na wykresie. Następny system wart rozważenia ma więc 16 zakładów, następny 24, 32, 48 itd. Ponieważ jednak opłacalność nie wzrośnie drastycznie, uważam, że na powyższym ośmiozakładowym systemie rozsądnie jest się zatrzymać. Przy okazji oczywiste spostrzeżenie: jednokrotna gra powyższym systemem na 8 zakładów jest dużo bardziej opłacalna od gry jednym zakładem na 8 losowań, przy jednakowym koszcie gry (24 zł).
Można oczywiście rozważać systemy, w których żetony są rozłożone jak najrównomierniej, ale bez nacisku na uzyskanie jak najwięcej opłacalnych wyników gry (pól ruletki), wobec czego występują duże prawdopodobieństwa małej straty (np. 3 zł) zamiast mniejszego prawdopodobieństwa niestracenia. Pozostawiam to jako ćwiczenie dla chętnych.
Dla czystej przyjemności przeanalizowałem jeszcze największy z systemów proponowanych przez Totalizatora, tzn. taki, w którym typujemy 12 liczb i zawieramy 924 zakłady. Nie będę go tu wypisywał, prosto go wygenerować. Kosztuje aż 2772 zł, a daje tylko 2,57% szans na zwrot tej sumy! (Teoretycznie najlepszy system 924-zakładowy miałby opłacalność równą 23%.) Pełna tabela wygranych jest bardzo krótka:
| Prawdopodobieństwo | Saldo (2M;3500;100) |
| 85,20% | -2 772 zł |
| 12,22% | -756 zł |
| 2,36% | 5 404 zł |
| 0,21% | 40 628 zł |
| 0,01% | 3 061 828 zł |
(Przy saldzie podane hipotetyczne wartości wygranych niższych stopni.) Czy słyszał kto o inwestycji 3 tysięcy złotych z 85% prawdopodobieństwem utraty całego wkładu?! (Nie należy oczekiwać, że przy wyższych wartościach czwórek lub piątek opłacalność się zmieni, bowiem w drugim wierszu tabeli wkład w saldo od czwórek i piątek jest zerowy.) Wnioski nasuwają się same. „Zagraj w Toto, idioto.”
Postscriptum. Skomplikowane gwarancje
Wielu ludzi nabiera się na tzw. systemy „gwarantowane”. System jak najbardziej może gwarantować jakąś wygraną i nie ma w tym niczego dziwnego. Np. ten system gwarantuje wygranie trójki. (Ale uwaga — ma bardzo niską opłacalność! Od 0,41% do 2,07% przy założeniu czwórki w granicach 100–300 zł.)
Tyle że wiele systemów „gwarantowanych” ma dodatkowe obwarowania. Na przykład: system gwarantuje trójkę o ile wypadnie 5 z 10 liczb występujących w systemie. W istocie oznacza to, że system niczego nie gwarantuje. W przeciwnym wypadku każdy system można by określić jako „gwarantowany” przy odpowiednich warunkach, włącznie z jednozakładowym systemem {1,2,3,4,5,6} (gwarancja szóstki przy 6 liczbach z 6 wytypowanych).
Przedstawiam tabelę prawdopodobieństw, pozwalającą przetłumaczyć warunek „trafionych ileś liczb z iluś” na konkretną wartość:
| Z Ilu \ Ile | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 100,00% | ||||||
| 1 | 87,76% | 12,24% | |||||
| 2 | 76,79% | 21,94% | 1,28% | ||||
| 3 | 66,98% | 29,41% | 3,50% | 0,11% | |||
| 4 | 58,25% | 34,95% | 6,39% | 0,41% | 0,01% | ||
| 5 | 50,48% | 38,83% | 9,71% | 0,95% | 0,03% | 0,00% | |
| 6 | 43,60% | 41,30% | 13,24% | 1,77% | 0,10% | 0,00% | 0,00% |
| 7 | 37,51% | 42,58% | 16,81% | 2,87% | 0,22% | 0,01% | 0,00% |
| 8 | 32,15% | 42,87% | 20,28% | 4,27% | 0,41% | 0,02% | 0,00% |
| 9 | 27,45% | 42,35% | 23,53% | 5,93% | 0,70% | 0,04% | 0,00% |
| 10 | 23,33% | 41,17% | 26,47% | 7,84% | 1,11% | 0,07% | 0,00% |
| 11 | 19,74% | 39,48% | 29,03% | 9,95% | 1,66% | 0,13% | 0,00% |
| 12 | 16,62% | 37,41% | 31,17% | 12,22% | 2,36% | 0,21% | 0,01% |
| 13 | 13,93% | 35,05% | 32,86% | 14,60% | 3,22% | 0,33% | 0,01% |
| 14 | 11,61% | 32,50% | 34,07% | 17,04% | 4,26% | 0,50% | 0,02% |
| 15 | 9,62% | 29,85% | 34,82% | 19,47% | 5,48% | 0,73% | 0,04% |
| 16 | 7,92% | 27,16% | 35,11% | 21,85% | 6,87% | 1,03% | 0,06% |
| 17 | 6,48% | 24,48% | 34,97% | 24,12% | 8,44% | 1,42% | 0,09% |
| 18 | 5,27% | 21,87% | 34,43% | 26,23% | 10,18% | 1,90% | 0,13% |
| 19 | 4,25% | 19,36% | 33,51% | 28,13% | 12,06% | 2,49% | 0,19% |
| 20 | 3,40% | 16,98% | 32,27% | 29,79% | 14,07% | 3,22% | 0,28% |
| 21 | 2,69% | 14,76% | 30,75% | 31,16% | 16,18% | 4,07% | 0,39% |
| 22 | 2,12% | 12,70% | 28,99% | 32,21% | 18,36% | 5,08% | 0,53% |
| 23 | 1,65% | 10,82% | 27,05% | 32,93% | 20,58% | 6,26% | 0,72% |
| 24 | 1,27% | 9,12% | 24,97% | 33,29% | 22,80% | 7,60% | 0,96% |
| 25 | 0,96% | 7,60% | 22,80% | 33,29% | 24,97% | 9,12% | 1,27% |
| 26 | 0,72% | 6,26% | 20,58% | 32,93% | 27,05% | 10,82% | 1,65% |
| 27 | 0,53% | 5,08% | 18,36% | 32,21% | 28,99% | 12,70% | 2,12% |
| 28 | 0,39% | 4,07% | 16,18% | 31,16% | 30,75% | 14,76% | 2,69% |
| 29 | 0,28% | 3,22% | 14,07% | 29,79% | 32,27% | 16,98% | 3,40% |
| 30 | 0,19% | 2,49% | 12,06% | 28,13% | 33,51% | 19,36% | 4,25% |
| 31 | 0,13% | 1,90% | 10,18% | 26,23% | 34,43% | 21,87% | 5,27% |
| 32 | 0,09% | 1,42% | 8,44% | 24,12% | 34,97% | 24,48% | 6,48% |
| 33 | 0,06% | 1,03% | 6,87% | 21,85% | 35,11% | 27,16% | 7,92% |
| 34 | 0,04% | 0,73% | 5,48% | 19,47% | 34,82% | 29,85% | 9,62% |
| 35 | 0,02% | 0,50% | 4,26% | 17,04% | 34,07% | 32,50% | 11,61% |
| 36 | 0,01% | 0,33% | 3,22% | 14,60% | 32,86% | 35,05% | 13,93% |
| 37 | 0,01% | 0,21% | 2,36% | 12,22% | 31,17% | 37,41% | 16,62% |
| 38 | 0,00% | 0,13% | 1,66% | 9,95% | 29,03% | 39,48% | 19,74% |
| 39 | 0,00% | 0,07% | 1,11% | 7,84% | 26,47% | 41,17% | 23,33% |
| 40 | 0,00% | 0,04% | 0,70% | 5,93% | 23,53% | 42,35% | 27,45% |
| 41 | 0,00% | 0,02% | 0,41% | 4,27% | 20,28% | 42,87% | 32,15% |
| 42 | 0,00% | 0,01% | 0,22% | 2,87% | 16,81% | 42,58% | 37,51% |
| 43 | 0,00% | 0,00% | 0,10% | 1,77% | 13,24% | 41,30% | 43,60% |
| 44 | 0,00% | 0,00% | 0,03% | 0,95% | 9,71% | 38,83% | 50,48% |
| 45 | 0,00% | 0,00% | 0,01% | 0,41% | 6,39% | 34,95% | 58,25% |
| 46 | 0,00% | 0,00% | 0,00% | 0,11% | 3,50% | 29,41% | 66,98% |
| 47 | 0,00% | 0,00% | 0,00% | 0,00% | 1,28% | 21,94% | 76,79% |
| 48 | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 12,24% | 87,76% |
| 49 | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 100,00% |

